Math, Learning, and Shame Traps

What’s holding us back?

Back when I taught college math, I tried my best to help students cultivate a true, deep understanding of what math was. It was nearly impossible to do within the bounds of the current metric-focused education system. I still tried.

Three groups of students started to form.

There was the group of students who cared about understanding the material—they may have considered themselves bad at math, but I didn’t think they were. These students thrived when given proper support. Wherever they started, they ended up in a stronger position than when they had entered my class. There were even a few students who had real talent, a real knack for proofs, but the education system had never given them credit for it, so I was able to right that wrong. Lovely to work with overall.

There were the students who didn’t really care about the material. They just wanted a grade so they could get a job—entirely understandable. We clashed sometimes, but I tried to do right by them too.

Then there was the third group, my white whale. These students loved what I had to say about logic at the beginning. They listened intently to my introduction on the philosophy of math, with the focus on formal reasoning, truth, exploration, iterative learning, and self-awareness.

Right up until they failed my first midterm.

Then they hated me.

This pattern seemed to repeat multiple times in my personal and professional life, and it confused me for years. I would be in what I thought was a good-faith discussion and then, for reasons that were beyond my understanding, someone would shut down and act defensive, as if I’d hurt them. I had no idea why. It kept happening. I mulled it over for months at a time, puzzling out why and what I could do to avoid it.

Now I’m somewhat satisfied with my analysis. It’s personal, and it’s incomplete, and it’s experimental, but it may be helpful to shed light on a particular social dynamic many of us have come across.

Today I’ll introduce that theory.

The Path to ‘I Know’

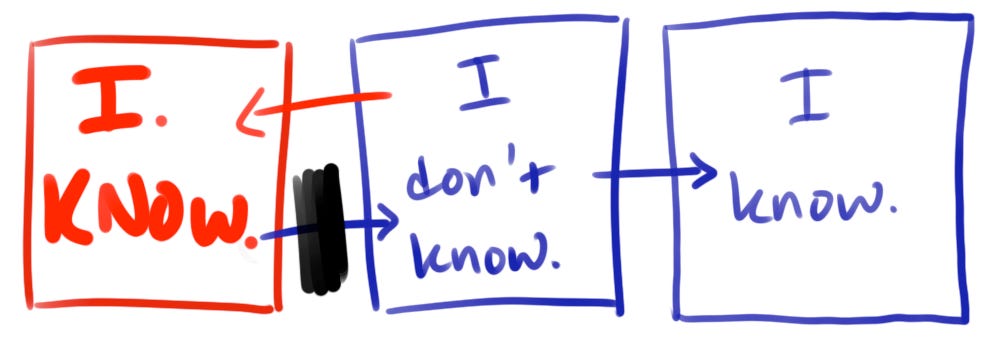
Consider how a person thinks when they’re exposed to a new concept.

Ideally, they know the concept is new to them, so they think, “I don’t understand this.”

This is the “beginner’s mindset,” and those who learn well know this is always the first step towards learning something new. The hope is, as the person gets more exposure to the concept, explores with it, plays around with it, they start to gain familiarity. They realize what works and what doesn’t, why it is the way it is, and over time, with each new bit of effort, they build confidence. The beginner’s mindset is an excellent place to be.

That arrow represents a heroic amount of time and brainpower. It has multiple steps, it can go backwards, it’s frustrating, but at the end, they will have gained something. The road is long and arduous, but students can get through it if they know they’ll be on steady ground by the end.

This is how math education is supposed to work.

This is not how math education works.

A student once asked me why we study proofs if we’re not going to use the results in real life. I told her, “because being able to figure out whether something is true will greatly improve your life. It will make you harder to trick, mislead, or confuse. Exploring these concepts in an abstract framework gives you a way to test things out that won’t hurt you if you get it wrong. You’re not going to lose any friends for not being able to derive a formula. You might if you fall for bad reasoning in real life, though.”

I’d missed something.

Math is understood as one of the purest fields of study, and students pick up on the intrinsic value of logic quickly. They learn to use math performance as a proxy for intelligence. The evaluation system teaches them to fixate on mistakes, since the reward system is based on grades. Every one of us has felt a pit drop in their gut at a marked-up test they thought they did well on, and the few people who can say they haven’t ever experienced a math-related blow to their ego either haven’t gone far enough or are great at processing their feelings.

Studying math is supposed to be either emotionally neutral or rewarding. But we’ve placed so much emphasis on STEM intelligence being the pinnacle of human knowledge, and value the concepts of Logic and Reason so highly, that it’s not.

The focus on arithmetic over proofs, as well, tricks people into thinking applying a process is “math,” when really the heart of mathematics is knowing where these processes come from. It makes sense from a practical perspective; arithmetic is easier to grade. But students being evaluated on arithmetic are trained to overlook the aspects of math that would benefit them the most. They internalize that being “smart” means knowing the answer—rather than being able to explore and derive the process that got them to the answer—and that getting something wrong makes you “stupid.”

It’s the opposite. Mistakes and false starts are necessary to fully understand a problem. Yet when grades are based on arithmetic, mistakes are seen as weakness. The best move to preserve one’s ego is to never go deeper. It’s no wonder some students stand at the beginning of a long and winding path, and declare themselves to have already walked it.

By the time they get to college, many don’t start off at “I don’t know.”

No, no.

It is so important to them to be seen as smart, and to have already mastered formal logic, that they have convinced themselves they have a special knack without having to work for it.

I call this a shame trap.

Shame traps

When I taught math, my goal was to help my students progress in their understanding, no matter where they started. But unfortunately, the first step to learning something is admitting you don’t already know it. There were many students who didn’t take that first step. I understand why, I truly do. With the amount of time and effort students invested into arithmetic, it would be incredibly painful to confront that they never understood concepts they thought they mastered. This wasn’t just an evaluation problem, this was an emotional block. Something they thought they could rely on, being taken away, would transform a point of pride into a source of weakness, shame, humiliation, and inadequacy.

That’s why I’m calling this defensiveness towards confronting a false perception or belief—in this case a Dunning-Kruger-flavored knowledge deficiency—a shame trap.

Shame trap: when the amount of emotional pain it would cause to abandon a false belief is so great, the individual clings to the false belief no matter how much it holds them back.

That is, the emotion keeping them there isn’t arrogance or pride, but rather shame. Shame is the emotion they have to process to move forward in the diagram. If students couldn’t process that shame, they resisted learning, while their classmates who thought they were “bad at math” could make progress.

I tried to address this in a productive way, but my formal training fell short. Mathematicians are taught to act as guides through a complex process, letting students walk the path and nudging them in the right direction when appropriate. That’s this arrow:

But helping students move forward from a false, internalized perception is much harder:

(Not every student who did poorly is in the red zone, either. Some stayed in the middle but felt too confused or hopeless to engage with the material. I consider this slightly different, although changes that help students in the red zone may benefit them as well.)

Someone focused on accuracy might think the first step is directly showing the belief-holder proof that decisively contradicts their perception. A failed test, a direct conversation, something that shows they’re not on solid ground yet. They then have all the evidence they need. The ball’s in their court, and changing course is their choice.

What I found, though, is that direct assessment was taken as aggressive. It didn’t give them the tools they needed to get out of the shame trap. The hope was that students could see the gap between how they viewed themselves and what the assessment said, but this process didn’t convince students to drop the ego and focus on the material itself. It only caused them to fixate on their negative emotions more, making the barrier to progress even higher.

It was like placing this big wall in front of the exit.

No matter how gentle I tried to be, no matter how many outs I gave, I could not figure out how to make the system work for these students. It’s not possible to process someone else’s emotions for them, or understand the material for them. But there are changes we could make to ease the burden.

The great irony, of course, is that the processes used in math—as well as the focus on discovery rather than shame—were what I used to pull myself over the exact same block.

So what can we do?

I left teaching and academia because the forces working against me were too great. I haven’t been able to find a place where I ‘fit in’ and can make money quite yet; many are hostile by default, and the pervasive shame traps are a huge reason why.

Regardless, I have had limited success creating small pockets where creativity and exploration can thrive, bringing hope to others, and challenging harmful, false beliefs in an indirect way that encourages readers to explore concepts instead of wallowing in negative emotions.

In the next few essays, I plan to discuss how to identify shame traps, how an individual can overcome the block, why it’s so hard to talk about shame traps without playing into a wider shame culture ourselves, and what we can do to restore what we’ve lost.